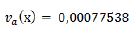Introducción:
- Trabajo.
- Metodología.
Problema 1: viga de sección constante:
- Definición problema.
- Planteamiento y desarrollo de la solución analítica.
- Planteamiento y desarrollo de la solución matricial.
Problema 2: viga de sección variable:
- Definición problema.
- Planteamiento y desarrollo de la solución analítica.
- Planteamiento y desarrollo de la solución matricial.
Conclusiones.
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
Introducción
En el marco actual, de globalización e internalización, la obra civil tiene un papel muy importante; responder a todos los problemas infraestructurales, a cualquier escala y en cualquier punto del globo terrestre. Grandes puentes, rascacielos, canales, profundos túneles y todo tipo de obras, que se deben construir en función de factores económicos, políticos, sociales, logísticos, pero sobretodo dentro de unos plazos.
El hecho de tener que diseñar grandes proyectos, de gran dificultad y en plazos determinados, ha significado que parte de los ingenieros de caminos junto con otros ingenieros de otras especialidades, buscasen y busquen maneras de realizar los cálculos estructurales de la manera más eficiente y rápida posible.
Y es aquí donde se enmarca el objetivo de este trabajo: en la familiarización, por parte del alumnado de Civil, con este tipo de programario que busca absorber estas necesidades.
En este caso, dentro de la asignatura de Análisis de Estructuras, en el temario de Análisis matricial, se ha escogido GID, como software a utilizar, y en concreto Kratos; que implementa la teoría de métodos numéricos para la resolución de problemas ingenieriles. Cabe mencionar que toda esta infraestructura informática ha sido diseñada y desarrollada por: Center for Numerical Methods in Engineering (CIMNE).
Así pues, a lo largo del presente trabajo se calcularán las flechas de dos ménsulas sometidas a una carga puntual. Se resolverán de manera analítica y mediante software, y posteriormente se compararán. Además, se buscará y se intentará que el error sea inferior al 1%.
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
Problema 1: viga de sección constante.
En el primer problema de los dos propuestos, se nos presenta una ménsula de sección constante, figura 1, sometida a una carga puntual en el extremo libre.
Aplicando la teoría impartida en la parte de deformación de vigas, es decir, usando la ecuación de la elástica, calcularemos la flecha del extremo sometido a la carga p.
Procedemos al cálculo mediante software:
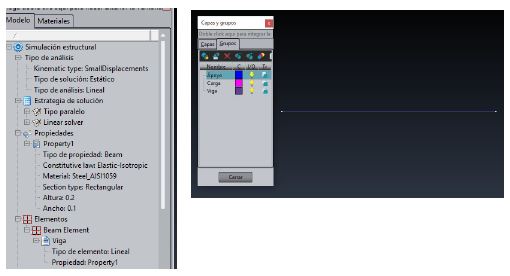
Primeramente, definiremos la geometría del cuerpo y los diferentes grupos que lo conforman.
Posteriormente, seleccionaremos las propiedades del material y daremos los valores de la sección. Cabe destacar que se ha seleccionado el acero AISI1059, que tiene un módulo de elasticidad de 200 GPa.
Seguidamente, introduciremos el valor de la carga, 1000.0 N en el sentido de la gravedad, y las condiciones de contorno del empotramiento empleadas son: desplazamientos y giros nulos en el apoyo.
Finalmente, se procede a generar la maya y a calcular los resultados, y estos se visualizan en el post-proceso, junto con la deformación.
Como último paso a realizar en este problema, se han comparado los resultados de los métodos, obteniendo un error nulo en la flecha del extremo libre de la ménsula. Por tanto, no es necesario hacer una gráfica (Nº Segmentos – Error).
La deformada final es la siguiente:
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
Problema 2: viga de sección variable.
De manera similar al problema anterior, primero se procederá a la resolución analítica y posteriormente a la resolución mediante Kratos. Finalmente se compararán los resultados.
En este caso tenemos una ménsula de sección no constante sometida a una carga puntual, de valor negativo de 1000.0 N en el extremo libre, figura 2.
Así pues, la ecuación de la deformada es:
En el extremo, el valor del descenso es el siguiente:
Procedemos al cálculo con Kratos:
En este apartado se han hecho sucesivas pruebas hasta encontrar el número de segmentos para obtener un error inferior al 1%. Así pues, se ha ido dividiendo la ménsula en segmentos: 1, 2, 4, 8, 12, etc. Hasta obtener un error inferior al 1%.
Cabe recordar que la ecuación de la recta es:
Se han seguido los mismos pasos que en el problema 1 para la obtención de los resultados y la deformada.
La deformada de la ménsula de sección variable, para 16 segmentos, es:
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
Conclusiones
En el primer caso, el error ha sido nulo, por que la flecha en los nodos de la malla es la misma que calculándola de manera analítica. La única diferencia está en los segmentos de la malla, que en este caso la flecha es una aproximación lineal. Por tanto, si solo te interesa saber la flecha en un punto, y la inercia es constante, es suficiente con generar una malla que tenga un nodo en el punto en qüestión.
En el segundo caso, a diferencia del primero, al ser la inercia variable, hay dos tipologías de errores: uno debido a la aproximación lineal (que solo nos afecta a la hora de determinar la flecha en puntos intermedios) y el otro error debido a que el programa solo calcula piezas con inercia constante. Por tanto, en este caso se tiene que dividir la pieza, y aunque para un problema sencillo como este el numero de segmentos importa poco, en un proyecto de mayor escala cuantos menos segmentos tengas que utilizar mejor.